はじめての図形描画 🔰
LibreLogo ツールバーで次の手順のとおりにアイコンを操作してみてください.
回数をまちがえないよう,声にだして数えながらやってみるとよいでしょう.
 (10 前進) を 4 回クリックします.
(10 前進) を 4 回クリックします.
 (15°右回転) を 6 回クリックします.
(15°右回転) を 6 回クリックします.
 (10 前進) を 4 回クリックします.
(10 前進) を 4 回クリックします.
 (15°右回転) を 6 回クリックします.
(15°右回転) を 6 回クリックします.
 (10 前進) を 4 回クリックします.
(10 前進) を 4 回クリックします.
 (15°右回転) を 6 回クリックします.
(15°右回転) を 6 回クリックします.
 (10 前進) を 4 回クリックします.
(10 前進) を 4 回クリックします.
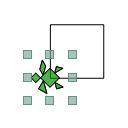 図1・出力される図形
図1・出力される図形
画面 (紙面) には図1 のような図形が出力されるはずです.
この図形は 4 辺が同じ長さで,となりあう 2 辺のなす角が 90°(直角) となっています.
このような図形には正方形という名前なまえがついていましたね.
したがって,先さきほどの手順はまとめて辺の長さ 40 ポイントの正方形を描えがくアルゴリズムと呼べそうです.
図1 で緑色みどりいろで描かれているのがタートル (亀かめ) です.
アイコンをクリックするたびにタートルが前進して線せんが描かれたり,タートルの向きが変かわったりするようすが観察かんさつできたでしょうか.
このように,タートルが紙面を動うごきまわったようすが図形として描かれるのがタートルグラフィックスの特長とくちょうです.
タートルグラフィックスのアルゴリズムを理解りかいするには,自分じぶんが浦島太郎うらしまたろうのようにタートルの背中せなかにまたがって紙面の上を動いているとイメージすることが大切たいせつです.
LibreLogo ツールバーのスクリーン初期化アイコンをクリックすると図形を消すことができますが,このときタートルの位置と向きは変かわらないことに注意ちゅういしてください.
ホームアイコンをクリックすると,タートルの位置と向きがはじめの状態に戻ります.
ホームアイコンだけをクリックしたときは,図形は消えずにタートルの位置と向きだけが変わります.
図1 ではタートルのまわりに,うすい色いろがついた小ちいさな四角しかくが 8 個こ描かれていますが,この小さな四角のことをハンドルと呼よびます.
ハンドルが表示された図形 (タートル) は選択せんたくされた状態になっていて,マウスでドラッグすることで位置を変えることができます.
タートルの位置を変えながら LibreLogo ツールバーのアイコンをクリックすることで,紙面にたくさんの図形を描くことができます.
タートルが選択された状態のときに,キーボードで Delete キーをタイプすると,タートルを消すこともできます.
さて,辺の長さ 40 ポイントの正方形を描くアルゴリズムで奇数きすう番目ばんめの「10前進」をクリックする回数を変えると,大おおきさの異ことなる (相似そうじな) 正方形を描くことができます.
その回数を :N 回と表あらわすことにしてみましょう.
また手順 3 以降は,手順 1 と手順 2 をくり返かえしているだけですので,次のようにまとめてしまうことができそうです.
- :N をいくつにするかを決めます.
- 次の操作を 4 回繰り返します.
 (10 前進) を :N 回クリックします.
(10 前進) を :N 回クリックします.
 (15°右回転) を 6 回クリックします.
(15°右回転) を 6 回クリックします.
この手順は辺の長さ :N ×10 ポイントの正方形を描くアルゴリズムと呼びましょう.
ここで,:N は変数へんすうと呼ばれます※1.
変数を理解するには「箱はこ」をおもいうかべて,その外側そとがわには :N というラベル (変数名へんすうめい) が書いてあり,箱の中なかに数値すうちが入っているとイメージするとよいでしょう.
このようにアルゴリズムを示しめすときに,特定とくていの値あたいに決きめておかずに,変数を使つかってあらわすと,いろいろな大きさの相似な図形を描けるので便利べんりですよね.
ちなみに,アルゴリズムを処理しょりしている間あいだには変更へんこうしない数のことは定数ていすうと呼ばれます.
興味きょうみがでてきた人ひとは,どんなものがアルゴリズムと呼べるのか,アルゴリズムはどんな性質せいしつをもつとよいのかなどについて調しらべてみましょう.
図形描画アルゴリズムを考かんがえてみよう 🔰
LibreLogo ツールバーのアイコンを使って,次のような四角形を描くアルゴリズムを考えてみましょう.
それぞれの図形の性質せいしつをよく思いだし,どんな変数を用意よういするとよいかもいっしょに考えましょう.
なお,変数は名前さえ同じにならなければ,いくつでも使うことができるものとします.
- 長方形ちょうほうけい
- ひし形がた
- 平行四辺形へいこうしへんけい
次に,LibreLogo ツールバーのアイコンを使って描ける正多角形せいたかくけいは何通なんとおりかを考え,それを描くアルゴリズムを考えてみましょう.
さいごに,台形だいけいを描くことができるか,描けない台形があるとしたらなぜなのか,考えてみましょう.
また,スタート地点ちてんとゴール地点がピッタリ重かさなる台形の条件じょうけんを説明せつめいしてみましょう.
 (10 前進) を 4 回クリックします.
(10 前進) を 4 回クリックします.
 (15°右回転) を 6 回クリックします.
(15°右回転) を 6 回クリックします.
 (10 前進) を 4 回クリックします.
(10 前進) を 4 回クリックします.
 (15°右回転) を 6 回クリックします.
(15°右回転) を 6 回クリックします.
 (10 前進) を 4 回クリックします.
(10 前進) を 4 回クリックします.
 (15°右回転) を 6 回クリックします.
(15°右回転) を 6 回クリックします.
 (10 前進) を 4 回クリックします.
(10 前進) を 4 回クリックします.

 (10 前進) を :N 回クリックします.
(10 前進) を :N 回クリックします.
 (15°右回転) を 6 回クリックします.
(15°右回転) を 6 回クリックします.